Geocoding
- CATRisk Consultants

- 31 ago 2020
- 13 Min. de lectura
Actualizado: 1 sept 2020
¿Qué es la geocodificación?
La geocodificación es el proceso de transformar una descripción de una ubicación (por ejemplo, un par de coordenadas, una dirección o un nombre de un lugar) en una ubicación de la superficie de la Tierra. Se puede geocodificar introduciendo una descripción de una ubicación a la vez o proporcionando muchas de ellas al mismo tiempo en una tabla. Las ubicaciones que se obtienen se transforman en entidades geográficas con atributos, que se pueden utilizar para la representación cartográfica o el para análisis espacial.

Con la geocodificación, puede buscar varios tipos de ubicaciones de manera rápida. Los tipos de ubicaciones que puede buscar incluyen: puntos de interés o nombres de un diccionario geográfico, como montañas, puentes y negocios; coordenadas basadas en latitud y longitud o en otros sistemas de referencia, por ejemplo, y direcciones, que pueden presentarse en varios estilos y formatos, por ejemplo, intersecciones de calles, números de casas junto con números de calles y códigos postales.
En la industria aseguradora es común el empleo de herramientas de geocodificación. Por ejemplo en el uso extendido de modelos de estimación de costes para riesgos de la naturaleza.
Las sumas aseguradas, y los valores de reconstrucción (TIV o Total Insured Value) deben incluir la localización geográfica o el territorio al que pertenecen. Esto es el código postal, el estado o región, las coordinadas de un sistema VRG (variable resolution grid)
P.ej. el sistema de modelización de RMS tiene diferente resolución para diferentes peligros naturales. 500 x 500 metros cuadricula para pelígro de huracán en Florida, EEUU. 100 x 100 km para riesgo de tornado o tormenta de granizo en el MedioOeste de EEUU, 10 x 10 km para tornados y tormentas en Oklahoma, lo más habitual es 5 x 5 km para otras zonas y-o peligros.
¿Para qué se puede utilizar la geocodificación?
Desde un simple análisis de datos, la administración de clientes y de negocios, hasta técnicas de distribución, existe un amplio rango de aplicaciones de la geocodificación. Con las direcciones geocodificadas, puede visualizar las ubicaciones de las direcciones espacialmente y reconocer patrones dentro de la información. Para ello, sólo debe ver la información o utilizar algunas de las herramientas de análisis disponibles en herramientas del tipo ArcGIS.
Los tipos de patrones que usualmente se cuestionan son por ejemplo, cuantas pólizas o contratos tienen asignado un valor correcto de 'geocoding', cuantos no han sido identificados, cuantos tienen asignado un código postal correcto o parámetros de latitud y longitud adecuados, cuantos por ejemplo tiene una dirección o calle valida. A veces la información se presenta en forma de sumas aseguradas agrupadas por zonas geográficas extensas, como una ciudad, o muy extensas como un estado o provincia. En algunos casos incluso por países enteros, p.ej. Arabia Saudita, norte o sur del país es lo mejor que se sabe.
Es por tanto el primer paso y el más importante asignar debidamente unas coordenadas. Será este mapeo el que luego determinará que peligros están asociados con esta región, y cúal es la vulnerabilidad de dicha linea de negocio; p.ej si las sumas aseguradas son de tipo residencial, o comercial, o industrial. o si por el contrario sabemos algo más como por ejemplo datos detallados del tipo de inmueble, como está construido, y cúal es su ocupación; es una vivienda unifamiliar, un bloque de apartamentos, una fábrica, un comercio pequeño, un restaurante, una industria farmaceútica, otro tipo de industria automobil, petrolifera, química, o puentes, carreteras, tendido eléctrico etc. Todas estas instalaciones se aseguran contra riesgos naturales.
Además de la modelización, en este punto tenemos un control p.ej. de la directiva de Solvencia II, tenemos todas los contratos incluidos en las previsiones de capital? qué porcentaje ha sido geocodificado correctamente? qué porcentaje de las sumas aseguradas está modelado asignando coordenadas, o latitud-longitud, y que porcentaje tiene errores. Todas estas preguntas determinarán la calidad estadística de la modelización (SQS Statistical Quality Standards del apartado de modelos externos en la directiva de Solvencia II).
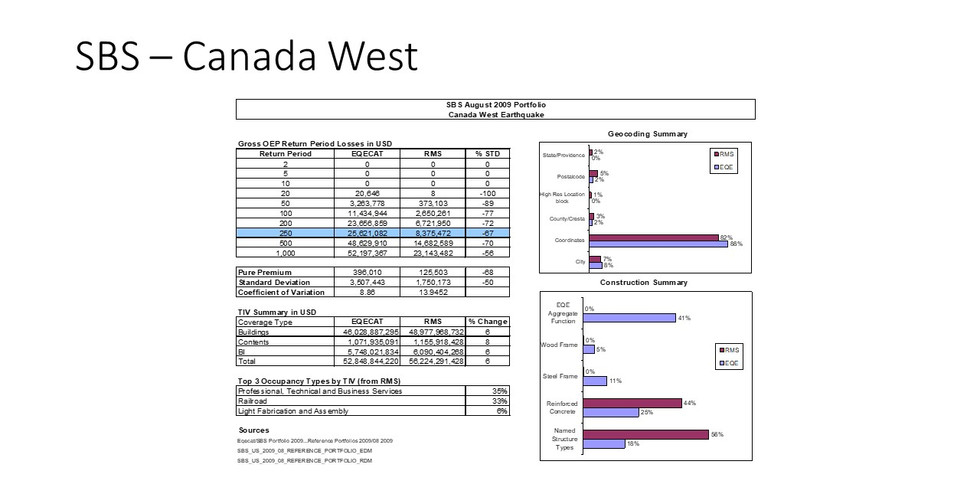
A continuación ejemplos por 'regiones' y 'peligros' de los porcentajes de geocodificación y vulnerabilidad asignada en los modelos de RMS y EQECAT que tienen incorporado un módulo de geocodificación.
Se puede apreciar que con herramientas distintas, este primer mapeo da resultados distintos. Es pues una de las variables de incertidumbre, ´geocoding´.
Un sistema de proyección geométrico, junto con un sistema de localización basado en coordenadas cartesianas, es decir basadas en un par de ejes ortonormales (X e Y), formando una cuadrícula, mejoraba la fiabilidad de distancias, áreas o ángulos medidos sobre los mapas, también llamadas coordenadas métricas . Un par de ejes son ortogonales si se cortan en ángulo recto, son normales si tienen la misma escala, y se denominan ortonormales cuando cumplen ambas condiciones.

La Tierra no es siquiera un objeto esférico sino que su forma se aproxima a un elipsoide o esferoide ligeramente achatado en los polos
Esta aproximación tampoco es válida cuando se desciende al detalle ya que la Tierra incluye numerosas irregularidades, se habla por tanto de Geoide para hacer referencia a la Tierra como objeto geométrico irregular.
Geodesia es la ciencia que estudia la forma y tamaño de la Tierra y las posiciones sobre la misma. La Geodesia define el geoide como una superficie en la que todos sus puntos experimentan la misma atracción gravitatoria siendo esta equivalente a la experimentada al nivel del mar. Debido a las diferentes densidades de los materiales que componen la corteza y el manto terreste y a alteraciones debidas a los movimientos isostáticos, esta superficie no es regular sino que contiene ondulaciones que alteran los cálculos de localizaciones y distancias.
Debido a esta irregularidad de la superficie terrestre, para describir la forma de la Tierra suelen utilizarse modelos de la misma denominados esferoides o elipsoides de referencia. Estos se definen mediante dos parámetros, el tamaño del semieje mayor (a) y el tamaño del semieje menor.
El achatamiento del esferoide se define entonces mediante un coeficiente como:
f = (a − b)/a
El achatamiento real de la Tierra es aproximadamente de 1/300. Alterando los valores de los coeficientes a y b se obtienen diferentes elipsoides.

Surge el concepto de datum que es el conjunto formado por los parámetros a y b del elipsoide, las coordenadas geográficas o angulares, latitud y longitud (λ y ω), del punto fundamental y la dirección que define el Norte.
Por ejemplo el datum europeo tiene como elipsoide de referencia el de Hayford, también llamado Internacional de 1924, y como punto fundamental Postdam (Alemania).
Los parámetros de este datum serían a=6378388 b=6356911.946
Punto fundamental: λ = 13o03058,74100E; ω = 52o22051,44600N
La dirección de referencia la definen los meridianos y se dirige hacia el Norte magnético
Establecer cual es el datum de un sistema de coordenadas es tarea de los servicios nacionales de geodesia. En España, el datum utilizado tradicionalmente en cartografía, tanto en los mapas del Servicio Geográfico del Ejercito (SGE) como en los del Instituto Geográfico Nacional (IGN), es el Europeo. Este puede ser el de 1950 si el mapa esta formado (información que se obtiene en la letra pequeña del margen del mapa) antes o durante 1979 o el europeo de 1979, si el mapa esta formado después de este año.
se busca que los datum tengan validez para todo el planeta, de forma que puedan tener empleo mundial, como el datum WGS-84 que suelen utilizar los Sistemas de Posicionamiento Global (GPS). Para ello se hace necesario un parámetro más que sería la distancia del centro del elipsoide con respecto al centro de masas de la Tierra.

Para definir latitud y longitud, debemos identificar el eje de rotación terrestre.
El plano perpendicular al eje de rotación que corta la Tierra atravesándola por su centro define el Ecuador en su intersección con el esferoide.
El resto de las lineas de intersección con la superficie terrestre de los infinitos planos perpendiculares al eje de rotación definen los diferentes paralelos o lineas de latitud constante.
Finalmente, los meridianos pueden definirse como las lineas de intersección con la superficie terrestre de los infinitos planos paralelos al eje de rotación o líneas de longitud constante.
Paralelos y meridianos se cruzan siempre en ángulo recto.
La longitud (λ) es la distancia angular entre el meridiano de un lugar y el de Greenwich, se expresa en grados, minutos y segundos de arco y se mide de 0 a 180o hacia el Este o hacia el Oeste desde el meridiano de Greeenwich.
La latitud (ω) es la distancia angular entre el paralelo de un lugar y el Ecuador, se expresa en las mismas unidades que la longitud y se mide de 0 a 90o hacia el Norte o el Sur. En ocasiones la latitud y longitud se expresan en grados y décimas de grado en lugar de en grados, minutos y segundos.
Un grado de meridiano equivale siempre a 111 kilómetros, mientras que un grado de paralelo equivale a 111cos(ω), es decir a 111 kilómetros en el Ecuador disminuyendo hasta 0 kilómetros en los polos.
La localización de un punto P sobre la superficie terrestre puede definirse de este modo mediante estos dos parámetros.
La ciudad de Murcia está, asumiendo el datum europeo, situada en λ = 1 grado 3 min 27 seg Oeste (W) y ω = 1 grado 3 min27 seg Norte. La letra W indica al oeste del meridiano de Greenwich y la letra N al Norte del Ecuador.
Las coordenadas de un hipotético rectángulo que enmarcara a España (excluyendo las islas Canarias) serían, en grados y décimas de grado: N: 43.80 N S: 35.82 S E: 4.33 E O: 9.29 O
En realidad, un grado de meridiano es ligeramente menor en el Ecuador (110.6 km) que en los polos (111.7 km) debido al achatamiento de la Tierra y, por tanto, de los elipsoides.
Latitud y longitud definen, por tanto, la posición de un punto sobre el esferoide de referencia del datum que se esté utilizando. Se considera que la superficie del esferoide coincide con el nivel del mar, así la distancia entre la superficie del esferoide y la superficie terestre en un punto cualquiera es su altitud.
Proyecciones
Cuando la distorsión debida a la esfericidad de la superficie terrestre se considera relevante se hace necesario buscar una ecuación que a cada par de coordenadas geográficas le asigne un par de coordenadas planas de manera que los diferentes elementos y objetos de la superficie terrestre puedan ser representados sobre un plano
Las unidades en que se expresa la longitud en estas nuevas coordenadas va a ser generalmente el metro, permitiendo, de cara a la incorporación de la cartografía UTM a un Sistema de Información Geográfica, el cálculo sencillo de variables de longitud, área o volumen de los elementos cartografiados expresados en unidades del Sistema Internacional.
Estas ecuaciones son de la forma:
x = f1(ω, λ)
y = f2(ω, λ)
Para obtener estas ecuaciones se proyecta la porción de la superficie terrestre que va a cartografiarse sobre una figura geométrica (un cilindro, un cono o un plano) que si puede transformarse en plano sin distorsiones. El foco de la proyección puede ubicarse en diferentes puntos dando lugar a diferentes tipos de proyecciones.
De este modo podemos clasificar las proyecciones en función del objeto geométrico utilizado para proyectar, se habla entonces de proyecciones cilíndricas, cónicas y azimutales o planas. En el caso de proyecciones cilíndricas o cónicas, la figura envuelve al elipsoide y, tras desenvolverla, el resultado será un plano en el que una parte de la Tierra se representan mediante un sistema de coordenadas cartesiano. En el caso de las proyecciones planas, el plano es tangente al elipsoide en un punto.
Un datum, asigna a cada punto sobre el Geoide un par de coordenadas angulares único y un sistema de proyección adjudica a cada uno de estos pares de coordenadas angulares un par de coordenadas cartesianas para su representación en un plano.
Desde un punto de vista matemático, se han definido diversos tipos de espacio, En primer lugar puede distinguirse entre espacios métricos y no métricos. Los primeros son aquellos en los que puede establecerse una medida de distancia a partir de la que pueden deducirse diversas propiedades métricas (área, perímetro, forma, etc.), pudiendo utilizarse diversas definiciones de distancia:
Distancia euclidea, responde al concepto tradicional de distancia como hipotenusa de un triángulo rectángulo. Es la más utilizada para resolver problemas geoespaciales:
di,j = [SUMA N k=1 (xk,i − xkj )] ^1/2
Distancia como distancia máxima, corresponde a la longitud del cateto más largo
di,j = maxN k=1(xk,i − xk,j )
Los espacios métricos deben cumplir una serie de condiciones:
Simetría: d(A, B) = d(B, A) d(A, B) <= d(A, C) + d(B, C)
Existen espacios no métricos que pueden resultar de interes trabajando con Sistemas de información geográfica, por ejemplo el tiempo necesario para recorrer el espacio entre dos puntos
Cuando se trabaja con cartografía digital es importante separar lo que son los datos espaciales, que deben ser lo más exactos posibles.
Sistemas de información
En general, un Sistema de Información (SI) consiste en la unión de información en formato digital y herramientas informáticas para su análisis con unos objetivos concretos dentro de una organización (empresa, administración, etc.). Un Sistema de Información Geográfica es un caso particular de Sistema de Información en el que la información aparece georreferenciada es decir incluye su posición en el espacio utilizando un sistema de coordenadas estandarizado resultado de una proyección cartográfica (generalmente UTM).
CARTOGRAFÍA DIGITAL
Introducción a los sistemas de información geográfica
Ayudar en la toma de decisiones empresariales.
En el caso del Sistema de Información de una compañía aérea, el sistema de reserva y venta de billetes debe actualizarse constantemente para permitir la consulta al mismo desde cualquier punto de venta. Toda esta información debe quedar almacenada para analizar la marcha de la compañía, cuantificar el impacto de determinados acontecimientos y apoyar decisiones como la compra de nuevos aparatos o la cancelación de vuelos.
Si pensamos en el Sistema de Información Geográfica de una región, este contendrá información ambiental y socioeconómica de manera que podamos consultar las características de un determinado espacio o cuales son las areas que cumplen con el conjunto de criterios recomendables para, por ejemplo, instalar un parque eólico. De este modo un Sistema de Información Geográfica se convierte en una herramienta fundamental para llevar a cabo estudios de Ordenación del Territorio o Evaluación de Impacto Ambiental.
De las diversas disciplinas que convergen en los Sistema de Información Geográfica, la cartografía es una de las que tiene una contribución más relevante. Los Sistema de Información Geográfica representan así una visión “cartográfica” del mundo apoyada en un espacio absoluto dotado de un sistema cartesiano de coordenadas obtenido a partir de un sistema de proyección. La fortaleza que supone el apoyo de la enorme tradición cartográfica implica también inconvenientes como el carácter estático y plano de los mapas y la incapacidad para reflejar el nivel de incertidumbe asociado a estos datos o la necesidad de unificar sistemas de proyección si los de las capas de información original son diferentes.
Bases de datos y consulta de datos
El lenguaje de consulta más utilizado en programas de gestión de bases de datos es SQL (Lenguaje Estructurado de Consultas). Sus resultados son tablas, sin embargo, estas tablas pueden combinarse con capas de información espacial preexistentes para obtener, como presentación, una nueva capa. Se hablará de la integración de Sistema de Información Geográfica con bases de datos. Los tipos básicos de consulta a un Sistema de Información Geográfica serían:
¿Que objeto aparece en el punto de coordenadas X e Y. ¿Cuáles son los valores de las variables V1, V2,... en dicho punto? ¿Qué puntos cumplen una determinada condición? Por ejemplo, tener una pendiente inferior al 5 % y no estar cultivados ¿Que entidades cumplen una determinada condición? Por ejemplo, cuantos embalses de la Cuenca del Segura superan el 50 % de su capacidad. ¿Qué relación hay entre los objetos A y B? Por ejemplo, ¿Está una determinada ciudad dentro del municipio de Murcia o de Cartagena? ¿Cual es la distancia entre dos puntos?
Un punto más allá de sofisticación sería la utilización de un Sistema de Información Geográfica para resolver problemas de toma de decisión en planificación física, ordenación territorial, estudios de impacto ambiental, etc. mediante el uso de instrucciones complejas del análisis espacial y álgebra de mapas.
En definitiva, se trataría de resolver preguntas del tipo:
¿Qué actividad es la más adecuada para un area concreta? Por ejemplo, cual es el uso del suelo más adecuado para una parcela concreta teniendo en cuenta una serie de criterios basados en variables espaciales de las que se cuenta con capas de información.
¿Cuál es el mejor lugar para la instalación de determinada actividad deseada (un centro de ocio) o indeseada (un vertedero)?
¿Cuál es la forma y tamaño adecuados de los espacios naturales para cumplir con sus funciones (por ejemplo, la conservación de biodiversidad)?
¿Cuál es la ubicación óptima de una red de torres de vigilancia forestal?
Finalmente, las aplicaciones más elaboradas de los Sistema de Información Geográfica son aquellas relacionadas con la integración de modelos matemáticos de procesos naturales, dinámicos y espacialmente distribuidos. Los objetivos perdeguidos puedn ser tanto científico como de planificación y ordenación.
Por ejemplo:
¿Qué áreas pueden inundarse en caso de producirse un episodio lluvioso dado? ¿Que consecuencias ambientales puede tener un embalse aguas abajo de su ubicación? ¿Cómo podría mejorarse la eficiencia en el uso del agua? ¿Cuál va a ser el impacto sobre el medio de dicha actividad?
Mientras que el resto de los objetos son más o menos perceptibles sobre el terreno o utilizando la cartografía apropiada, las superficies suelen ser mucho más difíciles de determinar, ya que en cada punto del territorio los valores son diferentes, al no disponer de un valor para cada punto, es necesario realizar una estimación. Es necesario recurrir a técnicas de interpolación. El ejemplo más típico de superficie es la elevación sobre el nivel del mar, representada mediante los Modelos Digitales de Elevaciones (MDE). Se trata de una superficie que representa la topografía del terreno, es decir, las alturas en cada punto de un territorio. Pero, en realidad, se puede crear superficies a partir de cualquier variable que cumpla unas mínimas características, esencialmente la continuidad espacial, sin que existan saltos bruscos en el valor de la variable. De este modo, diversos aspectos físicos naturales, tales como las precipitaciones, las temperaturas, la composición litológica o mineral, la acidez o basicidad de los suelos, etc., o también variables sociales: número de habitantes, densidad de población, etc., se pueden representar y analizar como una superficie.
DTM Digital Terrain Model for flood modelling
Uno de los elementos básicos de cualquier representación digital de la superficie terrestre son los Modelos Digitales de Terreno (MDT). Constituyen la base para un gran número de aplicaciones en ciencias de la Tierra, ambientales e ingenierías de diverso tipo. Se denomina MDT al conjunto de capas (generalmente raster) que representan distintas características de la superficie terrestre derivadas de una capa de elevaciones a la que se denomina Modelo Digital de Elevaciones (MDE). Aunque algunas definiciones incluyen dentro de los MDT prácticamente cualquier variable cuantitativa regionalizada, aquí se prefiere limitar el MDT al conjunto de capas derivadas del MDE. El trabajo con un MDT incluye las siguientes fases que no son necesariamente consecutivas en el tiempo: Generación del MDE Manipulación del MDE para obtener otras capas del MDT (pendiente, orientación, curvatura, etc.) Visualización en dos dimensiones o mediante levantamientos 3D de todas las capas para localizar errores Análisis del MDT (estadístico, morfométrico, etc.) Aplicación, por ejemplo como variable independiente en un modelo de regresión que haga una estimación de la temperatura a partir de la altitud Una de las razones por las que estas fases se solapan es que en muchos casos la manipulación, visualización y análisis van a permitir descubrir errores en el MDE. De este modo se vuelve a la primera fase y se genera un MDE mejorado.
Las variables incluidas en un MDT son factores de gran importancia en un gran número de procesos ambientales (precipitación, insolación-temperatura, flujos hídricos, erosión, distribución de hábitats, etc.) por tanto van a ser un elemento clave a la hora de estimar otras variables mediante procedimientos de interpolación global por regresión.
Fuente: Sistemas de Información geográfica.
rms.com


























































Comentarios