Tormentas del Sol y Magnetosfera: inundaciones y terremotos

las tormentas solares pueden causar graves peligros en los sistemas tecnológicos de nuestra civilización actual.

las tormentas solares pueden causar enormes daños en los sistemas tecnológicos de nuestra civilización actual. La denominada tormenta de Carrington, ocurrida en 1859, inutilizó las incipientes redes eléctricas y de telégrafos de Norteamérica y Europa. Se denominó así por el astrónomo inglés Richard Carrington, que fue el primero en observar una llamarada solar y relacionarla con las variaciones del campo geomagnético terrestre (Carrington, 1860). Los ejemplos modernos son numerosos. En marzo de 1989, una tormenta solar mucho menos intensa que la de 1859 inutilizó un transformador en Nueva Jersey dejando a 6 millones de personas en Quebec (Canadá) sin electricidad y provocando pérdidas de cientos de millones de dólares. Algunos países se han tomado en serio el riesgo de tormenta solar, como Estados Unidos. El 13 octubre de 2016, el entonces presidente de los Estados Unidos Barak Obama dictó la Orden Ejecutiva “Coordinating Efforts to Prepare the Nation for Space Weather Events” con el objeto de que todas las autoridades de EE.UU. estuviesen preparadas ante una hipotética tormenta solar de enorme intensidad.

En febrero de 2012, la Junta de Extremadura incluía en su plan territorial de protección civil un decálogo de recomendaciones para que los ciudadanos puedan estar preparados si ocurre una tormenta solar severa. Ese mismo año, en julio de 2012, pudo ocurrir un evento de meteorología espacial de extraordinaria magnitud. Sin embargo, la eyección de masa coronal no afectó de lleno a la Tierra.

Rotación del Sol

Para determinar el periodo de rotación solar se ha venido utilizando desde tiempos de Galileo las manchas solares de la “superficie” visible del Sol (la parte más baja de la atmósfera solar denominada fotosfera). Así, se puede establecer el periodo de rotación solar determinando el intervalo de tiempo entre dos pasos sucesivos m1 y m2 (Figura 1.1) de una mancha por el meridiano central del observador situado en la Tierra.

Ese periodo de rotación visto desde la Tierra se denomina rotación sinódica. Este periodo no es el verdadero periodo de rotación del Sol ya que la Tierra está orbitando alrededor del mismo. Mientras la mancha realiza una rotación sinódica con el Sol, la Tierra recorre un arco de la eclíptica, pasando del punto T1 al punto T2. En este tiempo, la Tierra se ha adelantado en su órbita, siendo por tanto la rotación sidérea menor que la rotación sinódica. Ya que el movimiento de la Tierra alrededor del Sol no es uniforme, el periodo de rotación sinódica depende de la parte de la eclíptica que recorre la Tierra alrededor del Sol entre T1 y T2, por lo que varía entre 27.20 y 27.33 días. El valor medio de la rotación sinódica es de unos 27.275 días.

El plano fundamental es el ecuador solar, que es el círculo máximo que contiene los puntos O y Ω. El eje de rotación del Sol es la línea PNC, que es perpendicular al plano del ecuador, la cual pasa por el centro del Sol (C) y corta a la esfera solar en PN, polo norte solar. Representamos también en la esfera del Sol el corte con la misma del plano de la eclíptica. Los planos de la eclíptica y del ecuador se cortan a lo largo de la línea CΩ (línea de los nodos), en la que el punto Ω es el nodo ascendente del Sol en el plano de la eclíptica. La línea Cπ es la línea perpendicular al plano de la eclíptica desde el centro del Sol. Esta línea forma un ángulo i con el eje del Sol, el mismo que forman los planos del ecuador y de la eclíptica en el punto Ω. Las líneas de dirección trazadas desde el centro del Sol (C) hacia la Tierra y hacia el equinoccio de primavera cortan la superficie del Sol en los puntos T y γ respectivamente. Nótese que estos puntos se sitúan en la eclíptica. El punto O, situado en el ecuador, es el punto origen de las longitudes solares. Este origen fue definido por Carrington como punto de corte de la eclíptica con el ecuador solar el 1 de enero de 1854 a medio día, fecha juliana 2398220.0. Es, por tanto, el punto que el 1 de enero de 1854 estaba en Ω, por lo que el punto O dista de Ω el valor del arco 12 M. Con este sistema de referencia es posible definir la posición de una mancha X sobre la superficie del Sol si se determinan la latitud y longitud heliográficas de la misma.

La latitud heliográfica de una mancha (B) es la distancia angular desde ecuador solar medida a lo largo de un arco de meridiano. Las latitudes serán positivas o negativas según se encuentre al norte o al sur respectivamente del ecuador solar con valores comprendidos entre 0º y ±90º. La longitud heliográfica (L) es el ángulo medido en el ecuador entre el punto origen (O) y el meridano que contiene la mancha. Su valor está comprendido entre 0º y 360º, y se mide en sentido directo.

El movimiento inercial solar es el movimiento del Sol alrededor del centro de masa del Sistema Solar debido a las posiciones variables de los planetas gigantes (J-Júpiter, S-Saturno, U-Urano, N-Neptuno). El Sol se mueve dentro de un área circular que tiene un diámetro de 0.02 AU (= 4.3 radios solares = 3.10^6 km). El Sol se mueve con una velocidad entre 9 y 16 m / s.

Descripción del movimiento baricéntrico del Sol

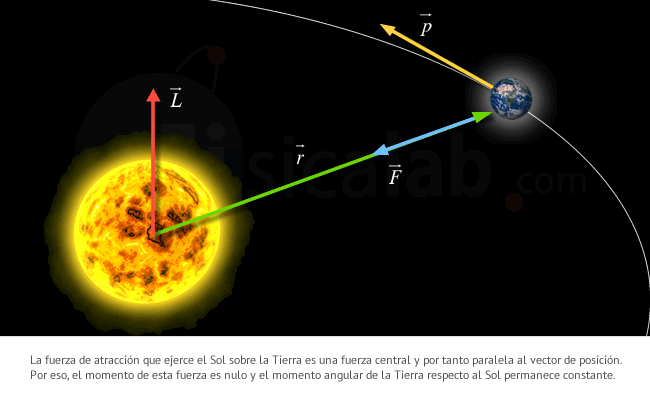
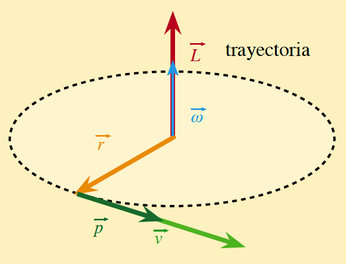
Cuando hablamos de rotaciones aparecen unas nuevas variables que ejercen un papel equivalente. Así, en lugar de desplazamientos, hablamos de giros. Donde antes usábamos distancias ahora usaremos ángulos. Donde antes teníamos velocidades, ahora serán velocidades angulares (velocidades de giro), w. Todas las fórmulas y relaciones matemáticas que se usaban para las traslaciones tendrán su equivalente en el mundo de las rotaciones. También la masa. Donde antes teníamos masa ahora juega su papel una nueva magnitud llamada momento de inercia, I. El momento de inercia de un cuerpo (por ejemplo, un planeta) que gira alrededor de un centro viene dado por mr2, donde m es la masa del cuerpo y r la distancia al centro de rotación. También existe una magnitud equivalente al momento lineal, es el momento angular, L, y comparte con el primero muchas de sus propiedades. El momento angular es un vector paralelo al eje de rotación. Siguiendo la analogía, será igual al momento de inercia multiplicado por la velocidad angular. De modo que la ecuación: p = m v, se convierte en: L = I w.

El ángulo de inclinación del eje de la Tierra con respecto a la eclíptica se denomina oblicuidad de la eclíptica ε que, como sabemos, es el responsable del cambio de estaciones, con un valor máximo de unos 23.5º. Cuando observamos el Sol desde el espacio exterior, vemos una proyección de la esfera solar sobre un plano perpendicular a la línea Sol-Tierra. La orbita solar se proyecta como una circunferencia, el disco solar se mueve en un cuadrado de aproximadamente 4.3 radii solares alrededor del centro de masa del sistema solar, debido a las posiciones variables de los planetas gigantes J-Jupiter y S-Saturno.

Movimiento de inercia solar e inundaciones en la República Checa

Las recientes y desastrosas inundaciones en la República Checa (Moravia 1997, Bohemia 2002) aumentaron el interés de los hidrólogos por las inundaciones históricas. Los datos más fiables están disponibles en la cuenca del río Vltava, porque la capital, Praga, se encuentra en el tramo inferior del río Vltava. En el último milenio se registraron veinte inundaciones desastrosas ordenadas en espiral en la imagen inferior, los puntos rojos son inundaciones en verano, y los azules de invierno. Ordenados según el ciclo 179 de la SIM.

Movimiento de Inercia del Sol

Charvátová (1988, 1990, 1997) dividió el SIM en dos tipos básicos, los ordenados en trébol según el orden de movimiento JS y el otro desordenado (caótico).

(Nota: las conjunciones de los planetas J y S ocurren una vez cada 19,86 años, y cada conjunción sucesiva avanza 117,3o en una dirección prograda.) En el caso del movimiento ordenado del trébol, el Sol orbita el centro de masa del sistema solar. a lo largo de un bucle (arco) aproximadamente una vez cada 10 años (JS / 2).

El Sol vuelve al trébol ordenado SIM después de 178,7 años y este tipo de movimiento dura unos 50 años.

Las partes más desordenadas del SIM se corresponden con los mínimos prolongados (Grandes disminuciones) de la actividad solar, durante el último milenio conocidos como mínimos de Wolf, Spörer, Maunder y Dalton.

Fuentes: Física solar, J.M. Nogales 2017

Charvátová, I., The solar motion and the variability of solar activity, Adv. Space Res., 8, 7, 147-150, 1988.

Charvátová, I., On the relation between solar motion and solar activity in the years 1730-1780 and 1910-60, Bull. Astr. Inst. Czech., 41, 200-204, 1990.

Charvátová, I., Solar-terrestrial and climatic variability during the last several millennia in relation to solar inertial motion, J.

Coastal Res., 17, 343-354, 1995.

Charvátová, I., Solar motion (main article), in: Encyclopedia of Planetary Sciences, (Eds. J.H. Shirley and R.W. Fairbridge), Chapman and Hall, New York, 748-751, 1997.

Charvátová, I., Can origin of the 2400-year cycle of solar activity be caused by solar inertial motion? Annales Geophysicae, 18, 399-405, 2000.