Determinación seismológica de la estructura de la Tierra.

El conocimiento de la estructura interna de la tierra sería primitivo si no hubiera terremotos. Se habrían reconocido fuentes explosivas de ondas elásticas y es posible debido a

1. Exploración sismología; dirigido a estructuras que contienen crudo en la corteza.

2. Las pruebas de armas nucleares más grandes generan ondas de amplitud suficiente para ser detectadas en estaciones remotas.

Las capas internas de la Tierra, así como la superficie, se aproximan a elipsoides achatados, simétricos con respecto al eje de rotación.

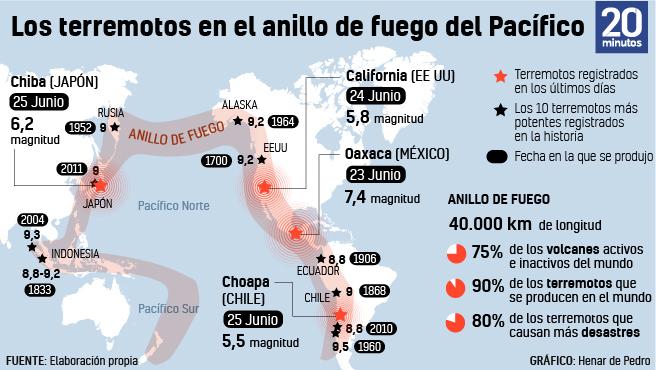
Grandes terremotos ocurren en sub-zonas limitadas alrededor de la tierra y estas sub-zonas obviamente difieren en algunos aspectos de las áreas no sísmicas más grandes.

Las ondas superficiales se propagan alrededor de la Tierra en trayectorias predominantemente continentales u oceánicas.

Prácticamente toda la información que tenemos sobre la elasticidad de la Tierra se obtiene a partir de observaciones de ondas sísmicas.

Distinguimos tres tipos de ondas, ondas del cuerpo terrestre, ondas superficiales y oscilaciones libres.

El problema de la era pre-nuclear

A finales de 1800, los geólogos estaban seriamente divididos sobre la validez de un cálculo sobre el enfriamiento de la Tierra, que imponía un límite a su edad.

Kelvin (1863) había demostrado que, si la Tierra se enfriaba por difusión del calor, a través de la corteza, entonces la corteza que aumentaba progresivamente tendría un gradiente de temperatura decreciente, alcanzando el estado actual después de 20 millones de años.

El actual flujo de calor de la Tierra (4,42 x 10 ^ 13 W) podría mantenerse para la edad actualmente estimada de aprox. 4,5 x 10 ^ 9 años con un enfriamiento total medio inferior a 1000 k.

Se entendia que la temperaturas internas de la tierra eran de cientos de miles de grados. La erosión del agua y sedimentación podrían haber ocurrido desde tan atrás como su calentamiento por el sol. Con anterioridad a los descubrimientos de las reacciones nucleares, no había mecanismos para mantener la irradiación solar durante el período considerado por los registros sedimentarios.

La única fuente importante de energía solar conocida por los físicos anteriores a la radiactividad fue el colapso gravitacional. Como sabemos ahora, esto fue necesario para elevar la temperatura del núcleo del Sol a los millones de grados necesarios para "encender" las reacciones de fusión nuclear.

La energía liberada por el colapso del Sol (masa M) a su radio actual, R, y estructura de densidad interna es:

Eg = KGM^2 / R (=6.6 x 10^41 J) donde K = 1.74 coeficiente numérico. Y G = constante gravitacional.

El modelo para la densidad del Sol en función del radio r. El radio exterior es = 6.9 x 10^8 km y la masa total es = 1.989 x 10^30 kg.

Estimación del momento de Inercia solar en función del radio r, el radio exterior rs

5.7 x 10 ^ 46 Kgm ^ 2

Para una esfera uniforme, K = 3/5 La energía sería 2.3x10 ^ 41 j

y entonces = KGM^2 / R (=6.6 x 10^41 J)

~ dE / dt = 4 .pi .radio^2 .S = 3.846 x 10 ^26 W actual pérdida de energía por radiación del Sol.

~ radio de la órbita de la Tierra

S = 1370 Wm ^ -2 es la constante solar:

la intensidad de la radiación a la distancia

/ -dE/dt = 1.7 x 10^15 s (la tasa actual de radiación, la energía gravitacional total duraría) = 54 millones de años.

El entendimiento generalizado era que las temperaturas internas son de varios miles de grados, por lo que la limitación no fue la insuficiencia de la fuente de calor, sino la lentitud de la difusión térmica en un cuerpo grande.

Las hipótesis de convección y conducción térmica mejorada fueron propuestas por Kelvin.

La erosión y la sedimentación causadas por el agua solo podrían haber ocurrido mientras la superficie de la Tierra estuviera calentada por el sol.

Antes del descubrimiento de las reacciones nucleares, no se conocían mecanismos para mantener la producción solar durante el período indicado por el registro sedimentario.

La única fuente importante de energía solar conocida antes de la radioactividad fue el colapso gravitacional.

Si asumiéramos el colapso de la energía, a una esfera uniforme, como en el cálculo original, obtendríamos 19 millones de años.

Todos estos resultados ignoran la energía térmica almacenada en el Sol, que es una gran parte de la energía gravitacional liberada y permite una estimación de la edad aún menor.

Hay dos modelos para la radiación solar

1. Geología sedimentaria

2. Colapso gravitacional

Y radioactividad (medición del calor radiogénico en rocas ígneas). También existen meteoritos que datan de hace unos 4,57 x 10 ^ 9 años y han sufrido pocas modificaciones.

No se puede obtener una edad independiente precisa para la Tierra a partir de rocas terrestres, que han evolucionado de muchas formas a partir de la mezcla nebular original.

Lo mejor que se puede afirmar es que una composición isotópica promedio de plomo en la corteza está cerca de la isócrona del meteorito (??).

Si el Sol fuera 100% de uranio, su calor radiogénico sería solo la mitad de la "producción solar" observada. El espectro solar era incompatible con un modelo tan extremo.

Fue con el reconocimiento de las reacciones termonucleares (1906), una capa de granito de 10 a 20 km proporcionaría suficiente calor radiogénico para explicar el flujo de calor de la tierra, sin necesidad del conocimiento de la profundidad de la Tierra en absoluto, y sugirió que la radioactividad se limitaba a una fina corteza químicamente distinta.

Otra sugerencia, la teoría de enfriar solo por difusión térmica (duró otros 60 años).

Finalmente, en 1960 y 1970 la teoría de la tectónica de placas y una historia térmica basada en un enfriamiento convectivo (es decir, el abandono de las ideas de Kelvin).

Sin embargo, la definición de la corteza terrestre se desarrolló a partir de la idea de Kelvin de una capa solidificada superpuesta a la roca fundida.

Propagación de ondas seísmicas

La deformación de las mareas y el período del bamboleo de Chandler brindan información que se extiende a bajas frecuencias, pero que carece del detalle y la precisión de la sismología.

Se puede considerar que las observaciones sismológicas se extienden hasta la frecuencia cero si se incluyen las deformaciones estáticas de los desplazamientos de los terremotos, pero el límite inferior de las frecuencias de las ondas sísmicas es 3 x 10 ^ 4 Hz, el período de 54 min del modo de oscilación libre oS2. En el otro extremo de la escala, las ondas con frecuencias del orden de 1Hz se registran en observatorios alejados de los terremotos que las generan.

Con este amplio rango de frecuencias, es necesario reconocer una ligera dependencia de la frecuencia de la elasticidad y la consiguiente dispersión de las ondas elásticas.

Sin tener en cuenta esto, hay una discrepancia pequeña, pero notable entre los modelos de la Tierra derivados de

1. Ondas del cuerpo terrestre de baja frecuencia.

2. Oscilaciones libres

Se reconoce la dependencia de la frecuencia que surge de la heterogeneidad.

Propiedades elásticas frente a longitudes de onda de ondas sísmicas (más corto que la escala de heterogeneidades introduce un problema de refracción / difracción local).

De nuevo, hay tres tipos de ondas, ondas de cuerpo terrestre, ondas superficiales y oscilaciones libres, aunque no hay una distinción clara entre ellas.

Las ondas del cuerpo terrestre de alta frecuencia tienen longitudes de onda cortas (en comparación con la curvatura de la Tierra).

+ propagación ~ (similitud) propagación de ondas bajas en un sistema óptico. Hay una analogía que conduce a los "rayos sísmicos" (normales a los frentes de onda).

Reflejada y refractada como rayos de luz.

No existe un equivalente óptico de las ondas p de compresión. Sí para las ondas S transversales de la sismología. Según consideremos ondas de frecuencias más y más bajas, con longitudes de onda correspondientes más y más largas. La teoría de los rayos de ondas del cuerpo terrestre será menos apropiada.

Para longitudes de onda que son fracciones significativas del radio de la Tierra, debemos considerar los modos normales de la Tierra como un todo.

Estas son las oscilaciones libres, ondas estacionarias de longitud de onda larga.

De manera similar, las ondas superficiales de longitud de onda larga se tratan mejor como modelos libres para los que se considera la esfericidad de la Tierra.

Las oscilaciones libres tienen un papel destacado en el modelado de la Tierra.

Ondas del cuerpo terrestre ~ (transmitidas) a través del interior de la Tierra.

En un cuerpo uniforme --------------> se extenderán como frentes de onda esféricos, dadas las heterogeneidades de la Tierra se reflejan y refractan de muchas formas.

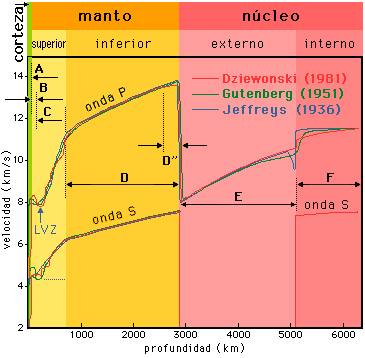
1. Las ondas P son primarias y la propagación es longitudinal.

2. Las ondas S son secundarias y la propagación es transversal. Estas ondas de compresión se refractan hacia adelante y hacia atrás transmitiendo como se expresa en la ecuación de onda.

Atenuación o decaimiento de las ondas

Las ondas p sísmicas planas satisfacen la ecuación de movimiento dada en forma general y considerar:

Estrés, medición y análisis de la corteza.

Un punto de partida básico es generar un modelo teórico de tensiones para encontrar soluciones que satisfagan las ecuaciones de movimiento. Las ecuaciones de movimiento en un medio continuo se encuentran aplicando la tercera ley de movimiento de Newton a volúmenes elementales sujetos a un campo estresado.

La 1ª ley establece: ∑F = 0 sí y sólo sí dv / dt = 0 (Fuerza neta = suma vectorial de todas las fuerzas que actúan sobre un objeto). Por tanto, la velocidad del objeto es constante o es un movimiento uniforme.

La segunda ley establece: F = dP / dt = d (mv) / dt y luego F = m. dv / dt = m.a solo es válido para un sistema de masa constante. La segunda ley implica la "conservación del momento" cuando la fuerza neta sobre el cuerpo es cero, el momento del cuerpo es constante. La fuerza aplicada sobre un objeto es el producto de la masa del objeto y su aceleración.

La 3ª ley establece: toda acción tiene una reacción igual y opuesta.

Consideramos un paralelepípedo de longitud δx y área de sección transversal δy δz.

La fuerza neta de este componente de tensión en el cuadrado frontal es:

F = F2 - F1 = δ/ δx (sigma xx) δx δy δz.

Si consideramos los esfuerzos cortantes de los otros dos lados de manera similar, obtenemos fuerzas adicionales:

en la dirección-x de δ/ δy (sigma yx) δy δx δy δz, y δ/ δz (sigma zx) δx δy δz.

Sumando estas fuerzas, la fuerza neta por unidad de volumen en la dirección x debida a la tensión impuesta sobre el paralelepípedo por el material exterior a él es igual a:

Fuerza / volumen = [δ/ δx (sigma xx) δx ]+ [δ/ δy (sigma yx) δy] + [δ/ δz (sigma zx) δx] = densidad x aceleración.

Además de estas fuerzas externas, el volumen puede estar sujeto a una fuerza interna del cuerpo por unidad de masa (g en el caso de la gravedad).

Entonces la fuerza por unidad de volumen es ρX.

La ecuación de movimiento se convierte en

fuerza / volumen = densidad x aceleración. Por tanto, el equilibrio de momentos implica la simetría de los componentes de la tensión. Resultados de ecuaciones de equilibrio.

Las ondas P sísmicas planas satisfacen la ecuación de movimiento, sin aceleración, en esta forma general en 3 dimensiones:

Para la propagación en una dirección (en un medio isotrópico) obtenemos

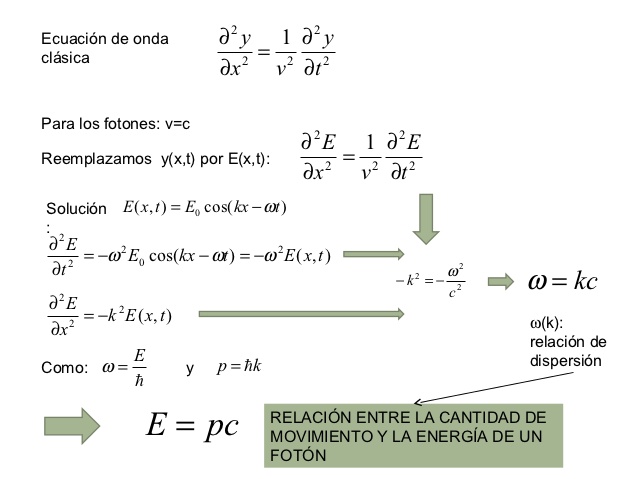
La ecuación de onda unidimensional en el eje ´x´para ondas mecánicas aplicada a ondas viajeras tiene la siguiente forma:

Donde x representa el desplazamiento espacial en esa coordenada, y v^2 representa la velocidad de la onda. P.ej en campos electromagnéticos esta constante sería c = la velocidad de la luz. La diferencial con respecto a t (tiempo) caracteriza la ecuación en cada eje espacial, en forma de vector gradiente.

La solución a la ecuación de onda es y(x,t) = A sin( kx - ωt + φ)

Los desplazamientos de partículas para una onda que viaja en la dirección x positiva se pueden escribir

y (x, t) = A exp (i (kx - ωt)) donde si no hay atenuación, el número de onda es

simplemente k = ω / c. Si el medio es atenuador, k es complejo.

Es conveniente retener k como componente real

y agregar un término imaginario = k + iα

Entonces podemos reescribir

U = Aexp(-αx)exp (i( kx – ωt)) que decae exponencialmente con la distancia.

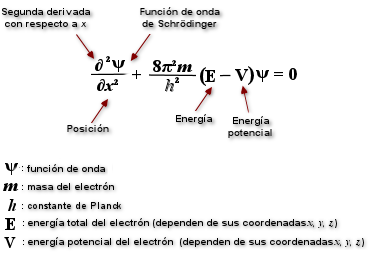
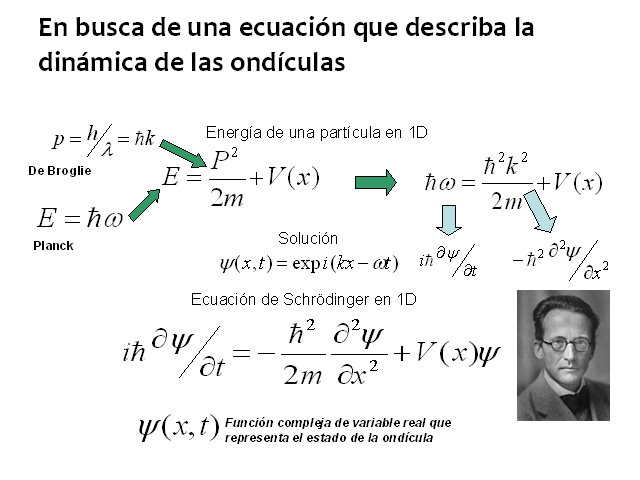
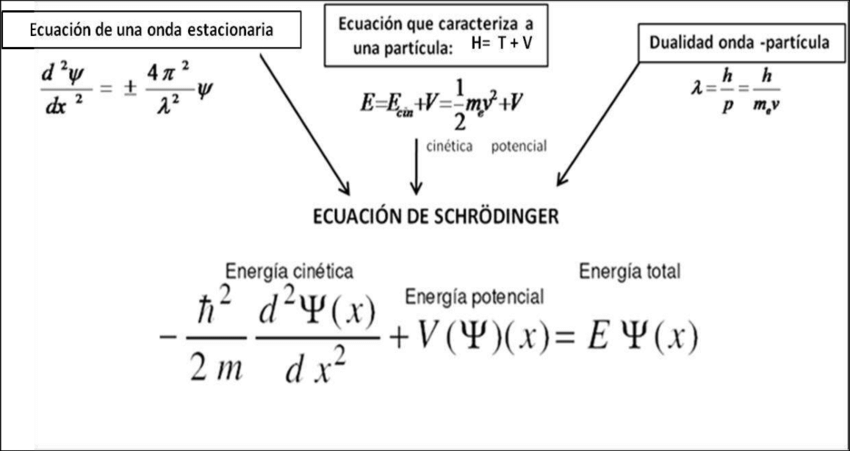
En mecánica cuántica la ecuación de onda corresponde a una función de probabilidad (introduce la dispersión en relación a la constante de Planck) evaluada como ecuación de movimiento de una onda-partícula por Schrodinger. La onda representa por tanto la probabilidad extendida a todo el espacio.

Esto se puede reescribir en términos de Q del medio como

U = Aexp(-αx)exp (i( kx – ωt))

donde α = ω / 2cQ es el componente de atenuación.

El problema de la dispersión relacionada con la atenuación es principalmente la aproximación de una constante, es decir, Q parámetro de frecuencia independiente relacionado con la pérdida fraccional de energía por ciclo.

2 π / Q donde Q es independiente de la amplitud de deformación, pero varía con la frecuencia ω / 2π. La energía de las ondas está relacionada con la amplitud.

La variación del módulo elástico con la frecuencia es dos veces más fuerte que la variación de la velocidad de fase, que depende de la raíz cuadrada del módulo elástico (la parte real de un módulo complejo con la parte imaginaria que representa la deformación π / 2 desfasada con la tensión).

Dado que las ondas de cuerpo tienen una ligera dispersión positiva (la velocidad de fase aumenta con la frecuencia).

Los componentes de onda de diferentes frecuencias no pueden viajar a la misma velocidad. Un coeficiente de atenuación dependiente de la frecuencia implica necesariamente también la velocidad o dispersión de la onda dependiente de la frecuencia.

En el caso especial de atenuación independiente de la frecuencia, es Q ~ ω (el parametro constante Q se aproxima a ω) no habría dispersión porque todos los componentes armónicos de un pulso se atenuarían de manera similar y se propagarían poco formados, pero con amplitud decreciente.

La amplitud también disminuye por dispersión geométrica. Un frente de onda curvado en expansión disminuyó en amplitud como 1 / radio de curvatura.

Por el contrario, un frente de onda de curva que se contrae concentra la energía. La variación de amplitud es simple si el radio de curvatura es muy grande en comparación con la longitud de onda, pero si no es así, entonces se requiere un tratamiento más general para tener en cuenta "la difracción".

Adoptamos la solución del "problema óptico" equivalente. La cantidad de enfoque depende de la relación entre la apertura y la longitud de onda, lambda.

A(0)/A(r0) = pi R^2 / r0.Lambda donde A(r) es la amplitud a una distancia r desde el foco, 2R es la apertura del frente de la onda en forma de casco esferico de radio de curvatura r0.

Una característica esencial de esta ecuación es el enfoque que depende de la longitud de onda. Esto no está relacionado con la dispersión y no requiere variación de frecuencia de la velocidad sísmica, pero es una consecuencia de la difracción.

Este fenómeno explica zonas o regiones de concentrada intensidad alta y peligrosa p.ej en Santa Mónica, California, observadas a causa del terremoto en Northridge M6.7 de 1994, que tuvo un epicentro a 21 km de distancia, demasiado distante para haber causado el daño sin un fuerte enfoque.

Santa Mónica se asienta sobre una profunda cuenca de sedimentos (~ 3 km) con una velocidad de onda S aproximadamente la mitad que las rocas ígneas en el subsuelo de los sedimentos.

Las irregularidades en el límite de la cuenca actúan como lentes, con dimensiones (aperturas) del orden de 1 km, centrándose en las olas que llegan sobre parches o regiones determinadas por la dirección de llegada de la onda. El enfoque depende de la frecuencia, lo que permite calcular las posiciones y dimensiones (aperturas) de varias de estas lentes.