Coordenadas baricéntricas (astronomía)
- CATRisk Consultants

- 27 sept 2020
- 4 Min. de lectura
Actualizado: 23 oct 2020
Las coordenadas baricéntricas tienen su origen en el centro de masas del sistema solar. Como el sistema solar es un sistema discreto se cumple:
Para simplificar consideremos sólo el planeta Júpiter que dista del Sol r = 778.330.000 km y tiene de masa Masa: 1.8981 x 10^27 kg y el Sol cuya masa es MS = 1,989 10^30 kg y cuyo radio es RS = 696.000 km.
El centro de masas distará del Sol una distancia x que está 46.403 km por encima de la superficie solar.

El eje de rotación de la Tierra está inclinado con respecto al polo de la eclíptica 23,45 grados. Esto nos da las estaciones. Pero el eje no mantiene una orientación constante en el espacio.

Las interacciones gravitacionales entre el ensanchamiento ecuatorial y la luna y el Sol provocan una precesión del eje alrededor del polo de la eclíptica. El eje describe un cono con un ángulo de 47 grados en un período de 25.730 años.
Para ver cómo surge la precesión, considere un pequeño satélite en una órbita circular que está inclinada hacia el plano ecuatorial. Dado que la Tierra no es esférica, su fuerza gravitacional sobre el satélite se dirige precisamente hacia el centro de la Tierra solo cuando el satélite está por encima del ecuador.
En latitudes intermedias, la variación de la fuerza gravitatoria debido a la latitud crea un torque o fuerza que tiende a tirar de la órbita del satélite hacia el plano ecuatorial, como un balancín.
Este torque o fuerza actúa en sentido perpendicular al vector de momento angular, causando una precesión de la órbita. Los puntos en los que la órbita cruza el plano ecuatorial se denominan nodos. Como se ve en el espacio, no en relación con la Tierra en rotación.
El ratio de la desviación es
J2 = 1.082 626 x 10^-3
Donde C y A son los momentos de inercia con respecto a los ejes polar, z, y ecuatorial, x y M, es la masa y a el radio ecuatorial. Hay un torque opuesto correspondiente en la Tierra.
El mismo principio se aplica al Sol y la Luna, pero en estos casos, hay un efecto notable en la Tierra. El torque, proporcional a (C-A), actúa sobre el momento angular de rotación de la Tierra, Cω, de modo que el ratio de precesión resultante proporciona una medida de la cantidad conocida como elipticidad dinámica.
Los dos factores principales del potencial gravitacional externo de la Tierra están dados por
V= +GM/r + G/r^3 (C- A) (3/2 cos^2 theta – ½)
1 / r es el dato principal, la segunda parte de la ecuación del potencial gravitatorio V, depende de la latitud, debido al ensanchamiento ecuatorial.
Además de la fuerza gravitacional central -m (dV / dr), ejercida sobre una masa m en (r, phi). Donde r es el radio desde el centro de la tierra a la superficie, y phi el angulo polar o desde un meridiano de referencia; normalmente Greenwich, hasta el punto de la superficie..
Se da un torque - m (dV / d phi), con otro correspondiente igual y opuesto ejercido por la masa en la tierra.
La magnitud del torque es proporcional a (m / r ^ 3).
La Luna y el Sol se equilibran por el torque que ejerce cuerpos en la Tierra dando lugar a la precesión del eje de rotación de la Tierra.
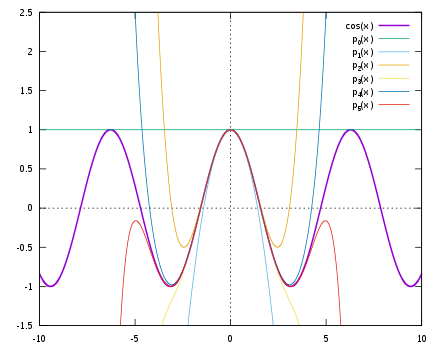
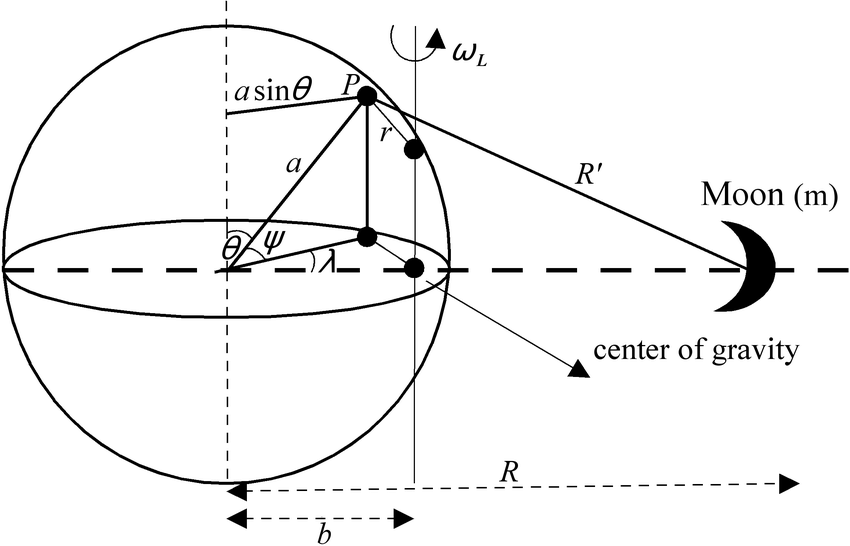
La causa del torque precesional se ilustra a continuación y la aproximación del cos por el desarrollo de Taylor para la distancia de la Tierra al Sol.
Dado el potencial gravitacional en el centro del Sol, masa Ms, instantáneamente en latitud geocéntrica phi y distancia R desde el centro de la Tierra. El potencial gravitacional en el centro del Sol debido a la Tierra viene dado por:
V= +GM/r + G/r^3 (C- A) (3/2 cos^2 theta – ½)
De modo que el torque ejercido sobre el Sol, y por lo tanto por el Sol sobre la Tierra, es
L = Ms dV/dphi = 3GMs/R^3 (C-A) sin phi cos phi
Este torque actúa alrededor de un eje en el plano ecuatorial normal a la línea Tierra-Sol, es decir, tiende a alinear el ensanchamiento con el eje Tierra-Sol en cada momento.
La conservación del momento angular en un sistema cerrado, como el Sistema Solar donde no se ejercen fuerzas exteriores a él, tiene la característica de hacer que las órbitas de los planetas sean planas. En efecto, como el vector, tanto su valor como su dirección, no cambia y el vector es paralelo al eje de giro, tenemos como consecuencia que el eje de giro no cambiará su dirección, no se inclinará, y por tanto la órbita seguirá siendo plana. Como el momento angular es el producto de I (=m r2) y w (la velocidad angular), vemos que será mayor cuanto: mayor sea la masa, mayor sea la distancia a la que gira y mayor sea la velocidad. De estas tres características tiende a dominar la distancia de giro, pues va elevada al cuadrado y un pequeño incremento en la distancia supone un gran incremento en el momento angular.
El momento angular de la Tierra en su movimiento de traslación alrededor del Sol. Datos: Periodo de traslación: 365,25 días Mtierra= 5,97 1024 kg Radio de la órbita alrededor del Sol: 149587 millones de km
Ahora ya podemos volver a la segunda objeción al modelo de formación planetaria de Laplace. Si tomamos el centro del Sol como punto de referencia para los momentos angulares de los cuerpos del Sistema Solar, al astro rey que gira lentamente en torno a sí mismo, a pesar de disponer del 99,9% de toda la masa del Sistema Solar, tan sólo le corresponde menos de un 1% del momento angular total del Sistema Solar. Los planetas tienen el 99% y pico restante. Sobresalen Júpiter con el 60% y Saturno con el 25%. La teoría de Laplace tenía serias dificultades para explicar estos valores.
Physics of the Earth, Frank Stacey chapter 6, 7, 16, 17












Comentarios